Category: server
06/29/08 09:35 - 69ºF - ID#44826
Estrip Downtime on thursday
Don't worry - nothing will go be lost - the server is just physically moving locations.
Permalink: Estrip_Downtime_on_thursday.html
Words: 64
Location: Buffalo, NY
Category: party
06/02/08 11:34 - 62ºF - ID#44527
Party On Saturday Night
Paul
Permalink: Party_On_Saturday_Night.html
Words: 17
Location: Buffalo, NY
Category: estrip
04/22/08 06:01 - 74ºF - ID#44104
Estrip short outage possible
Just a heads up, one of our two T1 circuits is totally out, so we're essentially running at half speed. Just in case you noticed any slowdowns, that'd be why... I just discovered there isn't so much as link lights from the telco on the circuit card so not good news...
I'm working with Level3 to see what's up - they did warn they might have to do "intrusive troubleshooting" - i.e. take the circuit offline and test it in loopback mode. Last time we had a problem like this, they insisted on testing the good circuit as well as the trouble one, leaving us totally disconnected... so if they go that route again there might be a brief (few minutes) of total outage. Here's to hoping not... that's all I know so far though, but figured I'd pass it on.
-Anthony
Artvoice
Permalink: Estrip_short_outage_possible.html
Words: 145
Location: Buffalo, NY
Category: stats
03/26/08 11:42 - 32ºF - ID#43803
Quick Stats Overview of Estrip
 stuff and I wanted to see what version of flash player people had to see if it was worth using Flex for estrip dev and I noticed that the Flash 9 player is used by 99%+ of userw. That is some seriously insane market penetration. Thanks youtube and xtube. I freakin love Flex. I am so excited about like more excited than I have been about anything web in so long.
stuff and I wanted to see what version of flash player people had to see if it was worth using Flex for estrip dev and I noticed that the Flash 9 player is used by 99%+ of userw. That is some seriously insane market penetration. Thanks youtube and xtube. I freakin love Flex. I am so excited about like more excited than I have been about anything web in so long.Here are some visitor stats
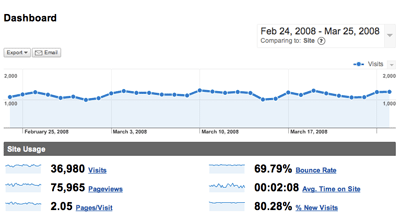
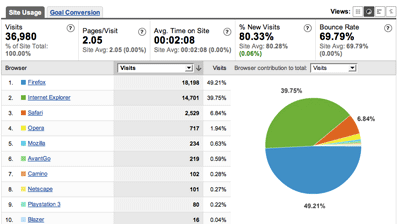
Notice that Firefox is now more popular than IE!
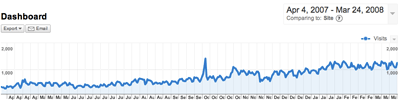
Over one year, the traffic is steadily growing.
Permalink: Quick_Stats_Overview_of_Estrip.html
Words: 112
Location: Buffalo, NY
Category: estrip
02/20/08 10:45 - 16ºF - ID#43411
I am a physician, blah, blah, blah
02/20/08 02:02@70.190.160.116 Guest wrote:
Hi do you guys have a webmaster? My name is coming up on a google search with slanderous material and I need to speak with the webmaster about this and hopefully remove this blog. Please e-mail me at jessica7273 AT yahoo.com I would very greatly appreciate this.
--- Paul Visco wrote:
> You would need to contact the user who wrote it. On
> each blog page there is
> a little yellow post it icon under the userpic.
> This allows you to message
> the user who wrote the post.
>
> Can you also send me a link to the page it is on. I
> can then take up the
> issue with the blogger.
>
> Thanks,
> paul
>
On Wed, Feb 20, 2008 at 12:26 PM, REMOVED EMAIL wrote:
The blog is over 1 year old, the girl who posted it is
severely mentally ill, she has been arrested for
attacking my mother and is being arraigned this week,
she hallucinates seeing me and we have a restraining
order against her. She is obsessed with me and I have
not had any contact with her in years nor do I intend
to contact her. I would prefer to not have to contact
my attorney to get this done. I have not lived in
Buffalo nor even visited there in years, I am married
with a husband as well as I am a physician. The
information on your blog is slanderous as well as a
defamation of character and I am assuming that you
have some control over what is posted. She apparently
is not a frequent blogger on your site rather has only
posted 1 random blog and as this comes up when you
google my name it should be removed. So please let me
know what other channels you have for this process.
Then I said:
I am willing to work with you on this. But if you do not give me the link to the blog, I cannot help you. How do you expect me to be able to locate the blog or the girl from the description you have given me in the last two contacts? Do you expect me to search for all blogs over 1 year old written by a girl.
Paul
Permalink: I_am_a_physician_blah_blah_blah.html
Words: 429
Location: Buffalo, NY
Category: artvoice
02/15/08 07:48 - 20ºF - ID#43350
Artvoice Best Of Buffalo 2008
There is a category for best blogger and I selfishly voted for myself. You can feel free to vote for yourselves.
--paul
Like the sound of (e:Terry)'s new hack and kill game with the girl with the red hair in the background? Sounds like I am reporting at some battle ground.
Permalink: Artvoice_Best_Of_Buffalo_2008.html
Words: 91
Location: Buffalo, NY
Category: estrip
02/07/08 02:32 - 33ºF - ID#43225
8 more comments till 30,00
Who would have thought that we had so much too say?!
Permalink: 8_more_comments_till_30_00.html
Words: 32
Location: Buffalo, NY
Category: web
02/03/08 11:51 - 32ºF - ID#43157
Cornering the Market on Search
buffalo blogs - estrip.org #1
I mean we come up in the top 5 for just about anything with buffalo or elmwood in the search term, but these are without.
Google Web Searches
warcraft sex - (e:shawnr,34230) #3
dong count - (e:jason,23538) #1
irresponsible dumb jerk - (e:theecarey,35835) #1
deinspiration - (e:imk2,37781) and (e:imk2,37795) #1 and #2
i don't like you that way - (e:theecarey,39212) #2 only after Idontlikeyouthatway.com
video liquidators - (e:paul,38302) #2 only to video-liquidators.com themselves
doctor fucking - (e:james,42894) #5
wegmans wifi - (e:paul,43004) #5
hypoallergenic dog breeds - (e:paul,32816) #7
nudist vacation adirondacks (e:paul,40394) #3
Google Images
There are a bizillion search combos we come up for. Some of the most popular are:
1900 house- Our living room comes up in row two
house buffalo, ny - our living room comes up along side the Darwin Martin and Coit house
linwood ave - our house is #1
nudist adirondacks - hm
naked adirondacks - hm
vermont ledges - hm
vermont ledges naked - hm
zoar valley naked - hm
Permalink: Cornering_the_Market_on_Search.html
Words: 188
Location: Buffalo, NY
Category: estrip
02/02/08 02:55 - 32ºF - ID#43139
100% of server fund has been raised
Paul

Permalink: 100_of_server_fund_has_been_raised.html
Words: 36
Location: Buffalo, NY
Category: buffalo
01/30/08 01:17 - 51ºF - ID#43089
NFTA Bus Schedules Made Easy - Buffalo
I decided to make a much simpler list for downloading the NFTA metro Bus and Rail schedules as I was so sick of navigating the stupid NFTA site to get the Bus schedule PDFs on my mobile. Its also at a simpler URL, estrip.org/nfta
 If you mobile doesn't do PDFS then this isn't so great but its still an easier way to load the PDFs on your computer for printing. Because of this I added a jpeg version as well. If you click the jpeg link next to a route, it converts the pdf to jpeg on the file for you so that you can view it with any image viewer. Maybe I will do a plain text version soon, if I have some time.
If you mobile doesn't do PDFS then this isn't so great but its still an easier way to load the PDFs on your computer for printing. Because of this I added a jpeg version as well. If you click the jpeg link next to a route, it converts the pdf to jpeg on the file for you so that you can view it with any image viewer. Maybe I will do a plain text version soon, if I have some time.It sucks that the schedules are in PDF format for most people but hopefully this at least makes them easier to get to. If I have time I might convert the data as well.

Download the NFTA metro rail and bus schedules for Buffalo, NY and save them somewhere

--Paul Visco
Permalink: NFTA_Bus_Schedules_Made_Easy_Buffalo.html
Words: 208
Location: Buffalo, NY
Author Info
Date Cloud
- 09/15
- 01/15
- 12/13
- 11/13
- 12/12
- 10/12
- 06/12
- 05/12
- 04/12
- 02/12
- 12/11
- 10/11
- 07/11
- 04/11
- 01/11
- 12/10
- 11/10
- 10/10
- 08/10
- 06/10
- 04/10
- 12/09
- 05/09
- 03/09
- 12/08
- 11/08
- 10/08
- 09/08
- 07/08
- 06/08
- 04/08
- 03/08
- 02/08
- 01/08
- 12/07
- 11/07
- 10/07
- 09/07
- 08/07
- 07/07
- 06/07
- 05/07
- 04/07
- 03/07
- 02/07
- 01/07
- 12/06
- 10/06
- 09/06
- 08/06
- 07/06
- 06/06
- 05/06
- 04/06
- 03/06
- 02/06
- 01/06
- 12/05
- 11/05
- 10/05
- 09/05
- 08/05
- 07/05
- 06/05
- 05/05
- 04/05
- 03/05
- 02/05
- 01/05
- 12/04
- 11/04
- 10/04
- 09/04
- 08/04
- 07/04
- 06/04
- 05/04
- 04/04
- 03/04
- 02/04
- 01/04
- 12/03
- 11/03
- 10/03
- 09/03
- 07/03
- 06/03
- 05/03
Category Cloud
More Entries
After This
My Fav Posts
- This user has zero favorite blogs selected ;(

 mobile
mobile

Uhm... do you mean Thursday or Tuesday? I can live without estrip *sob* honestly, i can...